The Impact Of Household Expectations In SFC Models

The importance of household expectations is one of the key differences between mainstream macroeconomic models and those in the stock-flow consistent (SFC) tradition. Since I do not think mainstream macroeconomic models are useful, I will not spend my time comparing the two competing approaches. Instead, I will just discuss how household expectations can be handled within SFC models.

One thing to keep in mind is that this discussion does not imply that the more general statement that expectations do not matter at all within SFC models. The role of expectations is extremely important when we turn to more realistic models of the business sector. The trends in fixed investment are a major cyclical driver, and they are driven by expectations. This is not easy to model; and it should be noted that business sector expectations are typically ignored within "workhorse" mainstream macroeconomic models.

Household expectations appear in Model SIMEX, described in Chapter 3 of Godley and Lavoie's Monetary Economics. The name reflects the fact that this is Model SIM (the simplest SFC model) which is augmented with the effect of expectations upon household consumption.

(I have discussed Model SIM in earlier article; for example, this article which discusses how to find the solution of the model equations. The simplicity of the model is partly the result of it treatment of the business sector. Within these models, the business sector reacts with perfect foresight to the actions of the household and government sector. Having more realistic business sector behaviour would require adding more model complexity, which is done later in Monetary Economics. I will be adding the ability to support this complexity within the Python sfc_models package over the coming months.)

The consumption function used within model SIMEX is (using the sfc_models variable naming):

DEM_GOOD = AlphaIncome * EXP_AfterTax + AlphaFin * LAG_F,

where: DEM_GOOD = demand for goods (i.e., consumption), EXP_AfterTax is the expected after-tax income, LAG_F = the previous period's financial asset holdings (denoted F within sfc_models), while AlphaIncome, AlphaFin are the propensity to consume out of income and wealth respectively. This is an "old Keynesian" consumption function, where it is driven by the current level of income and financial asset holdings.

By comparison, within Model SIM, the equation is:

DEM_GOOD = AlphaIncome * AfterTax + AlphaFin * LAG_F.

That is, the only difference is that Model SIM uses actual (realised) after-tax income, rather than expectations. Since after-tax income is determined by the simultaneous solution of all of the model equations within the period, Model SIM implies that the household has the ability to calculate exactly the current period model solution (and hence income). This is referred to as "perfect foresight," although it does not technically imply an ability to predict future outcomes.

Monetary Economics discusses two differing ways in which the expectations variable is determined. I will now discuss the first variant, which is labelled "SIMEX1" within the sfc_models package. In SIMEX1, the expected after-tax income is the previous period's realised after-tax income, or

EXP_AfterTax(k) = AfterTax(k-1).

(Within the earlier equations, the dependence upon the time axis ("(k)") is suppressed, following the
equation convention used within the Python package. As discussed below, this equation is only used for k>1, k=0 and k=1 are special cases. The variable k is used as the time step variable, as t is allowed to vary. For example, if we wanted quarterly data starting in 1950, we would set t=1950+0.25*k. In particular, this means that we always start at k=0 when discussing simulation results.)

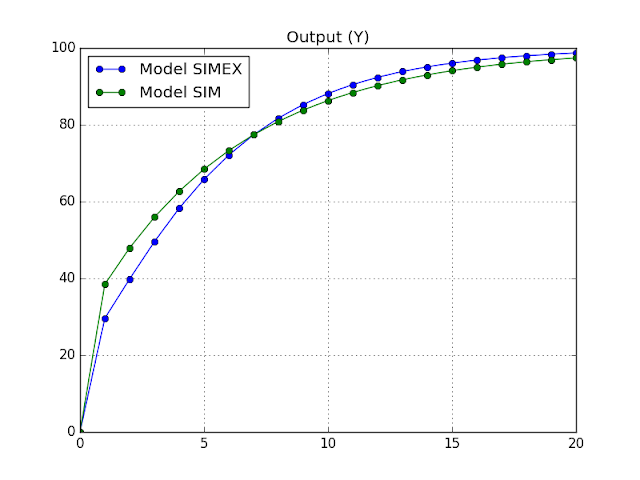
We will now look at example economic trajectory. The model starts off in a state of zero activity, and then the government starts activity moving by starting a programme of constant government purchases ("G") of $20 per period. The private sector responds, and aggregate output ("Y") converges towards  the steady state value of $100. (This means that the multiplier on G is 5; the simplicity of the model implies that government spending is the variable that determines the steady state output level.)

We can now examine the expected household after-tax income variable.

As can be seen in the chart, the expected income is just the previous period's income. At first, there is a large difference (forecast error), but the error decreases as the income converges towards its steady state value. (Please note that behaviour at the first time period -- k=0 -- is somewhat unusual; this is discussed below.)

The figure above shows the effect of using expected income rather than actual income in a model. We look at model SIM and SIMEX with the same behavioural parameters, and apply the same exogenous (external) input (government spending). In the earlier periods, the household sector reacts more quickly to the rise in income, and so aggregate output rises more quickly. As one might expect, the use of more accurate expectations results in a quicker response to policy changes. It should be noted that both models converge to the same steady state value. The reason why there is a crossover of the two time series around time period 7 is explained further below.

The counterpart to the miss in income expectations in spending is that the household sector's financial asset holdings evolve in a different fashion. Financial assets act as a cushion for errors in forecasting income and expenditures, a point which is emphasised in post-Keynesian writings.

The chart above shows the evolution of financial asset holdings by the household sector. Since the household sector is consistently under-estimating its income in Model SIMEX, it consumes less than in model SIM in the early time periods. As a result, it ends up greater financial asset holdings. Since spending also depends upon the stock of financial asset holdings, the consumption flow that is related to wealth is larger in SIMEX. By time period 8, this larger consumption flow out of assets means that output in SIMEX ends up being higher than in SIM. This is why there is the crossover in the figure that compares output Y between the models.

The role of financial assets is to act as a stabiliser within the model. Even with missed income expectations, the behaviour of the household sector still converges to the same steady state levels. The importance of such stock variables is the reason why these models are referred to as stock-flow consistent models; the name does not just imply that the accounting is done correctly.

Since the model converges towards the same steady state regardless of missed household expectations, we can see that these expectations are not extremely important for characterising how the model behaves. Admittedly, the response to the policy change is slower in model SIMEX than model SIM, but at the same time, the difference is much smaller than any errors we would get trying to fit model output to real world data.

There is a final technical point regarding the simulation results shown above. Model SIMEX in section 3.7.2 of Monetary Economics starts off with a special case for expected income. In period 1 of the book's simulations, the expected household income is not equal to the previous period's income (which was $0), rather it took into account the surge in government spending G. For period 1, the household assumes that total output is equal to G, and so its pre-tax income is equal to $20 (and the after-tax income is $16). It is only in later periods that the expected income is equal to the realised after-tax income.

This special case is simulated within Python code by forcing the realised after-tax income variable (HH_AfterTax) to be $16 at k=0. This is why the after-tax income is non-zero in the first period in the figure above. (I misinterpreted explanation for this special case when I read Monetary Economics; I would like to thank Marc Lavoie for patiently pointing out the passage that explains the special case.)

This workaround creates an inconsistency at k=0, but that is not viewed as problematic within the sfc_models framework: there is no attempt to solve the system of equations at k=0, and so it is sometimes preferable to drop that point from system output.

Code The Python code that generates the charts in this post is given by (requires the latest version of the sfc_models package):



As can be seen in the code, the meat of the model description is embedded within model builder objects that are found in the sfc_models.gl_book.chapter3 module. This is a feature that allows the user to quickly reconstruct the models within Monetary Economics. The source code that generates the underlying models is available for examination within the library. Furthermore, the model builder object gives the expected output, taken from tables in Monetary Economics. These expected output are used within unit tests that are used to validate the output of the sfc_models package. If someone makes a change to the package code that causes the actual output to deviate from the expected output, the unit tests will fail. This will developers to identity and roll back changes that cause the package to generate incorrect output.

Version 0.3.0 of sfc_models Released

I have released version 0.3.0 of the sfc_models package. The major developments in 0.3 versus 0.2 is a code base cleanup. The previously eccentric equation solution technique has been replaced with something more sensible, which greatly aids my ability to build tests to ensure the coherence of the system. There has also been a good amount of code refactoring, and the system for logging output is easier to work with.

With these programming workflow problems out of the way, it is easier to add new economic functionality. This analysis of model SIMEX was done very easily; the only problem I had was the result of my misreading the text regarding the setting of initial conditions.

Since I am using Monetary Economics to calibrate sfc_models, I now need to decide which chapter's models to tackle next. I could either take on models with bonds (Chapter 5), or open economy models (Chapter 6). My feeling is that the open economy model is more interesting.

Appendix - Sector Equations

The following are the sector equations created by sfc_models. Many of these are redundant, and get pruned from the system before solution is attempted. (If they are not, there can be convergence issues.)

Country: Code= "C1" C1
============================================================

[GOV] Government. FullCode = "GOV" 
------------------------------------------------------------
DEM_GOOD = EXOGENOUS [0.,] + [20.,] * 105
LAG_F = F (k -1 )
T = TF_T
F = LAG_F+T-DEM_GOOD
FISC_BAL = T -DEM_GOOD 

[HH] Household. FullCode = "HH" 
------------------------------------------------------------
DEM_GOOD = AlphaIncome *EXP_AfterTax +AlphaFin *LAG_F 
PreTax = SUP_LAB 
LAG_F = F (k -1 )
LAG_AfterTax = AfterTax (k -1 )
EXP_AfterTax = LAG_AfterTax 
AlphaFin = 0.4000 
AlphaIncome = 0.6000 
F = LAG_F-T+SUP_LAB-DEM_GOOD
T = TF_TaxRate * HH_PreTax
AfterTax = PreTax -T 
SUP_LAB =  BUS_DEM_LAB

[BUS] Business Sector. FullCode = "BUS" 
------------------------------------------------------------
PROF = 
LAG_F = F (k -1 )
F = LAG_F-DEM_LAB+SUP_GOOD
SUP_GOOD =  GOV_DEM_GOOD+ HH_DEM_GOOD
DEM_LAB = GOOD_SUP_GOOD

[TF] TaxFlow. FullCode = "TF" 
------------------------------------------------------------
TaxRate = 0.2000 
T = TF_TaxRate * HH_PreTax

[LAB] Labour market. FullCode = "LAB" 
------------------------------------------------------------
DEM_LAB =  BUS_DEM_LAB
SUP_LAB = DEM_LAB

[GOOD] Goods market. FullCode = "GOOD" 
------------------------------------------------------------
DEM_GOOD =  GOV_DEM_GOOD+ HH_DEM_GOOD
SUP_GOOD = DEM_GOOD

(c) Brian Romanchuk 2017