The model I discuss is taken from Chapter 3 of Monetary Economics. Although the explanation by Godley and Lavoie is the best discussion of mathematical economic models I have seen, it is still not completely obvious to a non-economist. For example, their "simple" model SIM has 11 variables to be determined, and the exact solution method was not obvious to first inspection. Some of this complexity is necessary -- even model SIM tracks the interactions of three sectors of the economy.

It took me time to get used to their style of working with the 11 variables in 11 equations; in control systems, all of these variables would be collapsed into vectors.However, it is advantageous as their exposition is similar to the rest of the academic economic literature.
It appears that academic economists like developing their models in the same way that circuit theory was taught when I took introductory electrical engineering courses in the early 1990s: you write down lots of equations, and then solve them via algebraic manipulations. (Given the inertia in undergraduate courses, I imagine that the same is still true.) Meanwhile, in the real world, electrical engineers simulate circuits by drawing them computer-aided design packages, and the circuit equations are solved via systematic use of matrix algebra.
Within this article, I am simplifying the discussion by only looking at how the solution is determined within the first period. The process I discuss would have to be repeated in later steps, but this would make things more complex. (I assume that the household sector starts with no money; that is no longer true after the first period.) Even this one-period calculation has hidden complexities.
UPDATE: The article "Techniques for Finding SFC Model Solutions" introduces techniques for solving these models without the simplifying assumptions made here. However, the discussion in this article helps provide an intuition with regards to the numerical solution techniques described there.
The extreme simplicity of this model cannot be emphasised enough: one cannot conclude anything about SFC models in general by looking at what this model alone can do. Within Godley and Lavoie, simplifications are eliminated in almost every direction.
 |
| Chart: Generated from Chapter 3 model of code by Raza and Kinsella |
In order to see what the full solutions look like, there is code available to solve the models in Godley and Lavoie at the "sfc-models" website: sfc-models.net. They now have R code, by Hamid Raza and Stephen Kinsella (which I used to generate the chart above; I have not had a chance to look at the code). That site has a good deal of Eviews code for various SFC models. Eviews is a commercial econometric package; I currently use R in my work here as it is open source.
The Pre-History Of The Model (t <0)
The model works in discrete time steps, labelled t=0,1,2,... These represent accounting periods, such as months, quarters, or even days. We have no notion of any data that is not at the model frequency. For example, if the model represents quarterly data, there is no way of representing monthly time series within the model. We follow mathematical convention and are starting the simulation at t=0.We assume that there is very little happening before t=0. There is no government money, and no economic activity, although we somehow have a labour force and capital in place at t=0. This is obviously unrealistic, but to be expected in a mathematical model.
If we look at how we solve at t=0, a solution with no activity is exactly what is predicted. Even though real resources existed, money (or more generally, financial assets) drives model economic activity. (In the real world, one would expect the private sector to create private money, but such an asset is precluded in model SIM.)
The Government Sector
The government starts issuing money at t=0. It kicks off economic activity by ordering $20 worth of services (produced by the business sector, as described below.)I am simplifying model SIM by assuming that government taxation is zero during the first period. (This means that the results I derive do not match the example values in the textbook.)
Since we are fixing government spending to be $20 for this period, and taxes are zero, we know that the government sector must run a fiscal deficit of $20 in the first period. The only financial asset within this economy is government money, and so we know that the private sector will hold $20 in money at the end of the period. (In model SIM, the amount of taxes levied depends upon economic activity. By eliminating taxation, solving the equations is much simpler.)
Household Sector
For simplicity, we assume that there is an unlimited number of workers available within the household sector. As a result, there is no concept of an "unemployment rate"; there is effectively an infinite number of unemployed potential workers, and a certain number of employed workers. We would need to model the labour market in order for the unemployment rate to have a realistic effect on the model solution.The implication is that workers are either employed full time or are unemployed. This is different than the convention in representative agent DSGE models, where all households are assumed to adjust their working hours based on the labour market situation. That is, an unemployment rate of 7% within one of these DSGE models is really households deciding to work hours that are 93% of "maximum employment" hours. The message is that if you are a household in a mathematical model, you want to live in a DSGE model, and not a post-Keynesian one.
The household sector works at the business sector, receiving wages. (In model SIM, it would also pay taxes based on wages received.) Not all wages are spent; some are saved and the household ends the period holding money. How much is saved is discussed below.
The Business Sector And Production
The business sector is assumed to hold capital (that does not depreciate) with infinite productive capacity; output is solely dependent upon labour inputs. Production is linear: for every worker hired, there will be an output of 1 unit of services. Services cannot be held in inventory, so the model is simplified as there is no need to track the stock (level) of inventories.
As is typical in a post-Keynesian model, prices are administered. This is done in an exceedingly simple fashion here, once again, for simplicity. (The model would be nonlinear if we violate this assumption.) The business firm has taken the notion of "non-profit" to an extreme, and pays workers $1 over the period, and charges $1 for one unit of output. (Since the worker produces 1 unit, the firm has exactly zero profit on every unit sold.)
The cash flows during the first period is illustrated below.
 |
| Flows in the simplified SIM model |
This implies a form of "model-consistent expectations," which is related to the concept of "rational expectations." The business sector has to accurately forecast its total revenue in order to determine the number of workers hired. If it did not, it could potentially incur a loss, which is assumed to be impossible.
There is a lot of arguments online about the use of "rational expectations" within models. Stock-Flow Consistent models can incorporate model-consistent expectations (as is assumed here), or expectation errors can be incorporated. As a result, SFC models are more flexible than mainstream models which assume that model-consistent expectations must always hold. Starting from this model, we could allow for business sector forecast errors if we added in business sector money holdings. At which point we also would need to introduce dividends (and possibly split the household sector into workers and capitalists).
"Accounting-Only" Model Solution
Since we assume that wage expense equals business sector revenue, we can inspect the diagram to see that the solution implies that the household sector saves $20. Beyond that, the model is still under-determined. That is, if all we do is insist that accounting relationships hold, there are an infinite number of solutions.- The business sector could hire 20 workers to produce the services demanded by the government, and those workers could save 100% of their wages. Total business revenue is $20.
- The business sector could hire 1000 workers, and those workers spend most of their wages ($980 out of $1000). Total business revenue is $1000.
Needless to say, this is somewhat unrealistic. Part of the lack of realism reflects the assumption about an infinite labour supply. Nevertheless, even if we modelled capital and labour constraints, there would be a range of solutions.
In other words, accounting relationships are not enough. We need to add a description of entity behaviour within the model.
Household Savings
The model needs a mechanism to pin down how much the household sector spends versus saves. (Looking at the previous diagram, we see that the household use of money is the only decision point within the model: all other flows are determined.) Stock-Flow Consistent models opt for fairly straightforward consumption functions. The standard functions used in Godley and Lavoie consist of fixed parameters multiplying disposable income (wages less taxes) and initial wealth (money) holdings.
For period t=0 in my simplified model, initial money holdings are 0, and so the consumption function is given by:
Consumption = a (Wages),
where 0 < a < 1.
For example, if a=0.6, we can back out that wages have to be $50, since the household savings of $20 is 40% of $50. (Full formula: Total Wages = $20/(1-a).) The lower the personal saving rate (higher a) the greater the level of wages and output. (Total output equals government and household consumption.)
The reason for my various simplifications of the model SIM is that it is possible to easily "read off" the solution for the system based on the fact that we know household savings equals $20. Otherwise, we need to solve the many equations of the system simultaneously to determine the solution. Given my aversion to masses of algebra, I would inevitably end up redeveloping the notation from scratch. This means that my version would no longer resemble the original solution method in Monetary Economics.
The reason for my various simplifications of the model SIM is that it is possible to easily "read off" the solution for the system based on the fact that we know household savings equals $20. Otherwise, we need to solve the many equations of the system simultaneously to determine the solution. Given my aversion to masses of algebra, I would inevitably end up redeveloping the notation from scratch. This means that my version would no longer resemble the original solution method in Monetary Economics.
From a multiplier perspective, $20 in government spending generates $50 in GDP. Given the linearity of various relationships within this model, GDP will scale up if government spending is scaled up. As Godley and Lavoie discuss, the model will converge towards a steady state -- if the government imposes a non-zero tax rate for t>0 (as shown below) -- and the steady state GDP will have an even higher multiplier. In other words, the "long run" multiplier for constant government spending is higher than the "short-run" (one period) multiplier.
[Update] There is an Excel file for simulating model SIM, by Javier López Bernardo (link to sfc-models page). As you can see, the spreadsheet is unhappy with my choice of a 0% tax rate (there is no steady state solution with a constantly growing deficit), but it shows that I did the math correctly for the first period (yay!). The screen shot above also shows the solution for the next accounting period as well.
For a longer view, the graph above depicts a couple of time series from the Excel model. The solution is blowing up, which is telling us that eliminating taxes from a model economy gives fairly nonsensical results. Returning the tax rate to the 20% used in the text gives more sensible looking results (shown below).
Excel Simulation
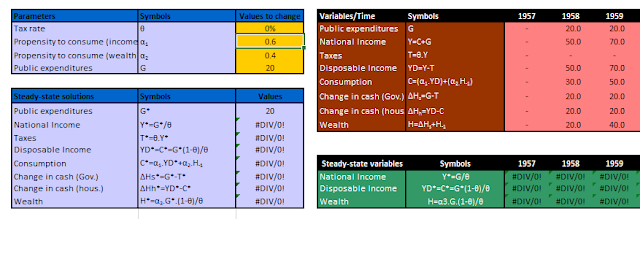 |
| Portion of Excel simulation by Javier López Bernardo (sf-models.net). (Solution continues to right.) |
[Update] There is an Excel file for simulating model SIM, by Javier López Bernardo (link to sfc-models page). As you can see, the spreadsheet is unhappy with my choice of a 0% tax rate (there is no steady state solution with a constantly growing deficit), but it shows that I did the math correctly for the first period (yay!). The screen shot above also shows the solution for the next accounting period as well.
 |
| Time series with no taxes |
 |
| Time series with a tax rate of 20% |
Expectations And The Time Period
The model developed was in discrete time, and there some unsettling implications about the multiplier process. (This discussion harks back to my article Discrete Time Models Are Not Frequency Invariant.) Can expectations adjust this quickly?
Imagine that the time period is daily. The business sector was previously mired in a state of no activity whatsoever. It suddenly receives a government contract for $20. Certainly, the recipient of the contract would quickly hire at least 20 workers. But would it hire an additional 30 workers that same day, on the basis of the expected circular flows of revenue within the economy? Moreover, in the real world, there are multiple firms, and revenue would be split up amongst them. Until revenue starts to come in, why would they start hiring?
This implausibility suggests that we should replace "perfect foresight" expectations with a version of expectations that allows for errors. (This is discussed in depth in Godley and Lavoie.) In this case, the multiplier effect would work with more of a lag. This would be particularly true if demand is met from inventories; firms can wait for inventories to be unusually depleted before ramping up production.
This implausibility suggests that we should replace "perfect foresight" expectations with a version of expectations that allows for errors. (This is discussed in depth in Godley and Lavoie.) In this case, the multiplier effect would work with more of a lag. This would be particularly true if demand is met from inventories; firms can wait for inventories to be unusually depleted before ramping up production.
Conversely, if the time period within the model is annual, businesses would notice increased activity during the year. One would expect hiring and output to ramp up within the model time step, and reach a steady state before the end of the accounting period. In such a case, model-consistent expectations may be a good approximation of reality.
These considerations mean that we cannot expect model dynamics to be similar across different model frequencies. That said, the difficulties faced by fitting these models to data are so large, that this is hardly our greatest worry.
If we compare SFC modelling to DSGE modelling, the clear advantage is held by SFC models (at least for those of us who have no interest in publishing in economic journals).
One can replicate almost all of the alleged advantages of DSGE models -- such as model-consistent expectations -- within a mathematical framework that is robust. Moreover, it allows for model behaviour that better matches empirical evidence from microeconomics (such as how prices are set by firms). Even if you hold the strong ideological belief that model behaviour must reflect optimising decisions by economic entities, you probably have a better chance of approximating that behaviour in a computationally tractable SFC model than in a DSGE model.
Concluding Remarks
It is an understatement to say that there are a lot of online arguments about the merits of differing approaches to macroeconomics. Some arguments are inherently political, but others revolve around seemingly esoteric model assumptions. (Although one could argue that there issues from political economy buried under those assumptions.)If we compare SFC modelling to DSGE modelling, the clear advantage is held by SFC models (at least for those of us who have no interest in publishing in economic journals).
One can replicate almost all of the alleged advantages of DSGE models -- such as model-consistent expectations -- within a mathematical framework that is robust. Moreover, it allows for model behaviour that better matches empirical evidence from microeconomics (such as how prices are set by firms). Even if you hold the strong ideological belief that model behaviour must reflect optimising decisions by economic entities, you probably have a better chance of approximating that behaviour in a computationally tractable SFC model than in a DSGE model.
See Also:
- sfc-models.net has code to solve the models in Godley and Lavoie.
- Techniques for Finding SFC Model Solutions
- My recent post - Modern Monetary Theory Not Modern - Sigh, which touches on the use of mathematics in Modern Monetary Theory. Modern Monetary Theory research uses SFC models to do mathematical analysis.
- My SFC/MMT resource page.
(c) Brian Romanchuk 2015

Another fine in-depth post. Thanks.
ReplyDeleteIt seems to me that you offer three snap-shot observations of the economy:
1. At t=0, there is no money.
2. At t=1, there is $20 held by government
3. At t=2, the $20 is distributed between business, households, and savings but government no longer has the $20.
I certainly agree when you say "We need to add a description of entity behaviour within the model."
It seems to me that we have no information what-so-ever about the path of the $20 or what activity it might have initiated. The only way to define the path of activity (for the $20) would be to build it into the model.
If we build the path into the model, we have only embodied our concepts into a mathematical or schematically correct description. Which, of course, can be of considerable value.
Although one could imagine a model which tracks the individual transactions, SFC models do not. The convention matches that of the national accounts: we have the sum of all the transactions during an accounting period, but we have no notion of the order of transactions.
DeleteWe have to think of all the transactions happening simultaneously, and we use the mathematics to pin down the size of the transactions. This is obviously related to how the mainstream thinks about "equilibrium", although I dislike how they use that term.
Thanks for a great article. I have such trouble understanding "models". Your post helps a lot.
ReplyDeleteI see the "sfc-models.net has code" link even has Excel files.
For me, that's perfect! Thanks.
Thanks. (For other readers, they also have Matlab files.)
DeleteThe Excel files might be good to work with for those who are allergic to algebra. (I actually dislike masses of algebra, as I prefer more compact notation.) It is useful to see how the results change as you change parameters, and you can dig into all of the numbers in the system. Spreadsheets are good for that type of exploration; but they are exceedingly unstable for ongoing work. I spent too much of my career ripping out malfunctioning spreadsheet code.
"Consumption = a (Wages)"
ReplyDelete(1-a) is the savings rate. Savings is being treated as if it were a tax which permanently removed money from the system. The $50-in-wages is the total private wage possible if every wage event is accompanied by 40% of the exchange going to savings.
The $20 is available in the next period (t=1). Having a non-zero cash balance makes the solution more complicated, which is why I only looked at this t=0 time step.
DeleteHowever, if we want to think of the $20 as 20 one-dollar bills, we see that they have circulated at least a couple of times within the accounting period, since total business revenue is $50. It is somewhat unclear how that infra-period circulation works, unless we pin down exactly the time frame of the period. We are never going to build a tractable model of every single transaction in an economy (unless we create something like a video game economy), so we cannot expect to pin down the exact sequence of transactions implied by the aggregate flows.
The code modules/spreadsheets I linked to solve the system for future time points.
"Until revenue starts to come in, why would they start hiring?"
ReplyDeleteOrders.
Companies don't start work at the point of revenue. They start work at the point there is a sniff of an order. In other words there is credit expansion via business credit.
The government order causes a cascade of orders without a single real dollar changing hands.
Very few of these models separate out the order and sales process from the settlement process. It's always cash and carry.
The orders would create a new asset to be tracked, which is precluded from the model. I did snot mention this as it was esoteric, but the system has only a single state variable that is tracked. That is, it is the simplest possible state space system, with a single state variable.
DeleteBut yes, once we allow credit, people can start spending before their wages arrive, etc.
Brian
ReplyDeleteFirst of all, thanks for your effort.
You wrote,
"For period t=0 in my simplified model, initial money holdings are 0, and so the consumption function is given by:
"Consumption = a (Wages),
"where 0 < a < 1.
"For example, if a=0.6, we can back out that wages have to be $50, since the household savings of $20 is 40% of $50. (Full formula: Total Wages = $20/(1-a).) The lower the personal saving rate (higher a) the greater the level of wages and output. (Total output equals government and household consumption.)"
Beyond the issue you acknowledged with the Excel workbook (which I downloaded), there is something I don't understand.
Consumption = a (Wages) means that Wages = disposable income (YD). But disposable income YD = (1 - theta) * Y. This means that theta = 0, which causes the Excel #DIV/0! problems.
But in addition to that, this is what I don't understand.
Given that theta = 0, 1/(1 - a) is the government spending multiplier (note that, by assumption, the consumption function has no autonomous consumption and apparently there is no gross investment).
Therefore, Total Wages = Y* = G*/(1-a) = $20/(1-0.6) = $50.
But the Excel workbook does not use the multiplier at all. It calculates Y* = G*/theta. Why?
More broadly, what is the value added of the charts, in comparison to the steady state values?
The steady state values are the values of the system as t gets larger. That is, if you look at the charts, they will converge towards those values.
DeleteThe value 50 (with no taxes) I calculate is a one-period "equilibrium" (G&L avoided that term, I believe; I am unsure how the concept here relates to the more mystical concept in mainstream macro). That is, if we solve the equations simultaneously, what solution do we get?
But when we go to t=1, there is now an initial stock of money. That adds another term to the consumption function, which increases output.
The steady-state values (with a *) were backed out with algebra; they are the values the system converges to. The steady state formulae are interesting in that they ignore the behavioural parameters, as you see. The reason is that in the steady state, the deficit is zero, and so we get that G* = (tax bill) = theta Y* = wage bill.
I will probably write another article about the steady state concept (unless I did already?). I am slowly summarizing the book...
Since I set taxes to zero, and spending is constant, the system never settled down, and there is no steady state. You need non-zero taxation to have steady state values.
Obviously, this is explained within the book; I am just covering the initial calculation step here. But even when I read the book, the solution method was not obvious, which is why I wrote this article. I will probably discuss why in a later article.
Thanks.
DeleteBrian, I think this post is the best primer on economic modeling that I have seen. Thanks.
ReplyDeleteThe simple model introduced is also a good vehicle to point out idiosyncrasies present in all models.
For example, in this simple model, each step comes to complete stability. The initial money injection moves into the hands of savers, where it stops at step end. For the next step, the savers spend all their money and get it back. The result is another $50 wage increment that is included in step two. This simple model would repeat this save-spend-save sequence over all additional time periods.
A second example of model idiosyncrasies is the point of injection of money into the system. Your simple model injects the money directly into the hands of workers, having been originated by government. Another choice of initial injection could have been the purchase of inventory-on-hand, or yet another point, directly into the hands of savers.
Both examples are choices of the model builder. Of course the choice made will affect the results of the model.
Yes - everything depends upon the model builder.
DeleteTechnically, the model has the government buying services from the business sector; it is not a transfer. A transfer payment to households can be modelled. It increases disposable income, and then the increased income is split between consumption/saving. I have not played with the Excel spreadsheet to know how easy it is to make that modification.
My models (haven't published them recently) actually have the government sector hiring workers instead of purchasing from the business sector. My models have a more realistic unemployment simulation, and so the effect is different.
DeleteVery good Brian. BTW, it's easy to see why it blows up if you set theta=0 for every period if you do the algebra: you essentially put a pole at 0 (continuous time), or at 1 (discrete time), thus the system becomes a pure integrator (time constant = infinity). If anybody's interested I have the expressions in text in the lower left of my interactive spreadsheet here. It'd be easy to add a theta column so that one could overwrite theta for any particular sample period (like the 1st, for example, to match your result with theta=0).
ReplyDeleteNote that you don't even need to do any algebra: it's right there in G&L's equations:
DeleteΔH = G - T
If T = 0 every period then
ΔH = G = a unit step scaled by 20
Thus H = integrated ΔH = a ramp climbing forever as t->inf
The lack of algebra was why I set the tax rate to zero...
DeleteThe algebra here was not too complex, but solving systems equation-by-equation is not systematic enough. That's why I am averse to pulling out the pencil and paper to solve the system. Academics like closed-form solutions, but I gave up on that after doing everything closed form in my thesis.
As an addendum for readers, the SFC academic community uses EViews, which allows you to enter equations directly into a solver, and then it cranks out a solution (somehow; probably iterative, would need to find the technical documentation). If you do not have Eviews (like myself), this does not help you find the algorithm to solve the system. But if you have Eviews, you can solve these systems in a somewhat systematic fashion.
DeleteIn this case, the relationships are linear, and one can cast it into a canonical form for a linear state space system (after some matrix algebra):
x(t+1) = A x(t) + B u(t).
However, any number of changes will make the system nonlinear, and you have to use some numerical techniques to solve the system.
This comment has been removed by the author.
Delete"after some matrix algebra"
DeleteActually you don't need any matrices for SIM: A and B are scalars here.
"...any number of changes will make the system nonlinear, and you have to use some numerical techniques to solve the system."
I've actually used the free online version of Excel to solve vector Newton iterations in making an interactive version of one of Nick Edmond's models. I fixed the number of iterations ahead of time (I used six per time sample). It was a bit of a pain, but it worked and I tried to set it up so it could be reused for a different model.
... I'm sure EViews is much easier!
DeleteBrian, Jason has drawn an analogy between SFC models and RLC (resistance, inductance, capacitance) circuits. He selected Fig 1 of this Wikipedia article, with a voltage source v(t) in series with resistor R, inductor L and capacitor C, and then solves for current i(t).
ReplyDeleteLining that up with SIM (G&L's SIM), I say you can make an analog computer out of that circuit if (for example) you get rid of the capacitor and replace it with a short (a wire) and just leave R and L. Here's one way to program the analog computer (forgetting about all the outputs and just concentrating on h (the continuous time equivalent of H, where h(n*T) = H[n], and g'(n*T) = G(n)):
di/dt = -(R/L)*i + (1/L)*v
is the analog computer for
dh/dt = a*h + b*g'
With the following equivalences:
h(t) in dollars = i(t) in amps
g'(t) in dollars/period = v(t) in volts
Ts = 1 "period" = 1 second
R = 0.25 ohms
L = 1.496521 henrys
Of course to make it correspond exactly to G&L's example at each sample time (0 sec, 1 sec, 2 sec, etc), v(t) should be a 20 volt step:
v(t) = 20 volts for t >=0, and v(t) = 0 for t < 0
But it can match G&L for any v(t) that stays constant between sample times.
... Ah, it looks like you've already found the post. Do you agree with my analog computer programing? Of course you can easily scale that to different electrical circuit times (other than 1 sec = 1 G&L period), so it's not unique in that sense, but given a particular electrical period, the solution is unique (for R and L). And of course you could switch v for i, or use difference correspondences (scalings) there too or make an RC circuit instead of an RL, etc.
Probably no one cares, but my 1st link is wrong. It should have been this.
DeleteMy dad did a project using an analog computer when he was in university -- in the 1950s. (Economists actually used hydraulic analog computers.) We may or may not have had exercises doing simulations in one of our labs in the 1980s, but analog computing is somewhat dated...
DeleteThe discrete time system for SIM has a single state variable, with a certain rise time. You would have to tune your RLC circuit to match that rise time, based on your arbitrary sample frequency. You cannot fix all 3 of R,L,C, which Jason suggests, since you could then only simulate a single discrete time system (if we fix the sampling frequency).
Even though I trained as an electrical engineer -- why would we care? There is an infinite number of models whose behaviour can be captured by the same state space model. However, there is no reason for those systems to have anything else in common.
This comment has been removed by the author.
DeleteOops. I mixed up your work and Jason's; I see that you had only one state variable. Deleted the misleading comment.
DeleteYes, I know they're dated. I actually used one in my undergrad EE course. Lol... Probably the last year that was required.
DeleteI no longer have access to an oscilloscope, so analog computing is definitely out for me. (Unless I do a Phillips(?) water model...)
DeleteSimulating a continuous time analog computer on a digital computer, so that I can use it to simulate a discrete time model sounds like something I would have done as a grad student after too many pints.
A water model... or perhaps a mass, spring and dashpot? (All you need for SIM are the spring and the dashpot... or the mass and the dashpot). Gotta have that dashpot thought! Lol
DeleteMaybe the "water" model is better... especially if it's not water.
The Cambridge Engineering department got a version of Phillip's hydraulic analog models working awhile ago, and had a video. Looked at it quickly (trying to see if I recognized anyone...).
DeleteBrian, you might be interested in this brief comment (I worked out exactly how determine SIM's parameters given both a desired steady state and a system time constant Tc)
DeleteOK.
DeleteHow are you generating the HTML for equations in a comment? When I looked into equation formatting, it involved addins that might not work everywhere.
MathJax. Look at the source for my page, search for MathJax, and then copy the lines you find (I think just one) at the top of your HTML editor page. I got mine from Jason. If somebody has that on their page, you can leave formatted comments on their page as well. One drawback: you loose your dollar sign. Anybody inadvertently putting a dollar sign in your comments will wonder what happened to their comment... it'll get screwed up.
DeleteAlso, the Chrome browser on my android phone has trouble with some of the superscripts (they don't always appear in their entirety). Android Firefox works fine.
DeleteAlso, AFAIK, you have to include that MathJax line in the HTML of every separate blog page you want it in. The good part is you won't mess up existing posts or comments which contain dollar signs. For example, I have a mix of pages: some with MathJax and some without. Also, there's probably a way to use a different escape character sequence... check the MathJax website.
DeleteOK, thanks. I looked at MathJax a couple of years ago, and the lack of support on some browsers made me avoid it. I'll try it out, and see whether people can follow it.
DeleteI took a good look at the model last night.
ReplyDeletePlease comment on my interpretation.
The excel sim takes two decay rates, one for taxes and one for savings. Decay removes money from the system with each transaction.
The tax rate is applied to the first transaction which reduces the remainder available for building consumption IN THE FIRST PERIOD.
The entire remainder (12.3) is assigned to savings.
The amount of tax collected provides the measure of consumption, with a limit of C = T/theta. THIS SETS THE RESULTS FOR THE FIRST PERIOD.
Beginning in the second period, a portion of household savings is added to (unchanged) government spending. The tax rate is applied to this sum and the identical sequence followed again. THIS SETS THE RESULTS FOR THE SECOND PERIOD.
This sequence is repeated until taxes equal the initial jump in government spending. At that point, the system has returned to stability at a higher level of consumption and wealth.
I believe we could think of this as a system with two stabilizing forces, taxes and savings.
Exactly.
DeleteWithout either, the model could produce infinite output; money recirculates at an infinite speed between households and business, and there are no real constraints in this model. In order to pin down a solution, money needs to be drained from income. This is done by taxes and savings.
In this case, a representative household assumption may be more "reasonable". What limits output in that framework is the fact that households can only work 24 hours a day...
Thanks
ReplyDeleteWell, this post, excellent though it is, does not answer my question of the working of the Keynesian multiplier within each time period. G&L do not spell it out, except that they indicate that it is what is in macroeconomic textbooks, and that the textbooks assume, unlike G&L, that it gives the only equilibrium value for Y. G&L assume that it produces only a short term equilibrium within each time period. Anyway, they don't spell the process out, and nobody seems to care. {shrug}
ReplyDeleteFor this model, the exact details would depend upon the time period. If the period were comparable to the payroll frequency, it would be very difficult to the system to adjust to government spending as a result of changing cash flows, rather it would have to rely on expectations.
DeleteIf the time period is one year, expectations would matter less. As workers spend more money, the firm would need to hire more people, and so the activity would be growing within the time period. The process then continues, and so the model activity grows during the second relative to the first.
It needs to be kept in mind that this is the simplest possible model. The working of the multiplier would be more interesting in more advanced cases. The key is that business sector decisions with regards to investment and inventory will then show up.
Thanks, Brian. :)
DeleteG&L do refer to two equilibria, one short term (within each time period) and one long term (steady state) (p. 70). They say that the periods could be years, quarters, or months. (Footnote 10, p. 72). I was sort of surprised that the short term equilibrium could be reached in one month.
OC, the use of time periods is unrealistic, since both equilibrium processes should be occurring at the same time. But I understand the pedagogical value of separating them.
BTW, Jason Smith ignores the short term equilibrium process, which makes him think that he has discovered a flaw in all the G&L models, namely that the velocity of money within each time period is 1. {shrug}
I looked at the book again when I started this article series, and I believe that they avoided the term "equilibrium." Within macroeconomics, the term is fairly meaningless at this point. The "steady state" term they use makes more sense, although it can be tricky to formally define in a growing economy (ratios go to a steady state, but individual variables are growing).
DeleteThe "in-period" equilibrium could represent practically any behaviour within the period. All that we know is that there is a solution to the equations. Although it's not completely supported by their discussion, one could argue that any number of micro behaviour schemes could be consistent with the equations, at least within an approximation error. (I am reading Anwar Shaikh's "Capitalism", and he discusses how different micro behaviours have emergent properties as a result of accounting constraints, and so they all end up with similar macro properties. However, Shaikh is somewhat critical of post-Keynesian models, so I am not saying that he endorses this model; rather I think one could draw a parallel to his analysis. I will be reviewing his book shortly.)
This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDelete