Side Effects Of Stability Of DSGE Models

The stability of the solutions of workhorse dynamic stochastic general equilibrium (DGSE) models is a major drawback of these models when trying to explain recessions. This article looks at the estimated linear New Keynesian model that was used in the previous discussion of the estimation of r* -- the Holston-Laubach-Williams (HLW) model. 

As I have noted a few times previously, more interesting behaviour can be obtained by nonlinear DSGE models. However, this flexibility comes at the cost of increasing the difficulty of fitting the model to data. There is an infinite number of models one can use to tell stories with.

Cut Down Model Dynamics

The New York Federal Reserve bank has a web page dedicated to r* estimation algorithms, which includes results as well as working papers detailing the algorithms: https://www.newyorkfed.org/research/policy/rstar. Although the linearised version of the HLW model is already much simpler than the nonlinear New Keynesian models, I will simplify things even further here. Since my concern is recessions, I am interested in GDP dynamics, and can put inflation to the side.

The HLW model is based on an output gap, which is he deviation of real GDP from trend GDP (both expressed as logarithms). Trend GDP has a growth rate that is subject to random deviations, but the trend growth rate changes are relatively small (and effectively ignored here).

The preferred way of expressing the output gap is the deviation of (log) real GDP (y[t]) from the trend level (y*[t]). In order to avoid dealing with fancy decorated values, I will denote the output gap as o[t]. (I use square brackets to denote a discrete time axis.)

Re-working the notation and using the coefficient values based on the current estimation, the dynamic equation of interest (equation [4] in Measuring the Natural Rate of Interest: International Trends and Determinants by Kathryn Holston, Thomas Laubach, and John C. Williams) becomes:

o[k] = 1.549 o[k-1] - 0.608 o[k-2] + v[k] + e[k].

where:

• o[k] = output gap (= 100(y[k] - y*[k])),
• v[k] = effect of interest rates (described below),
• e[k] = external random disturbance.

The effect of interest rates (v[k]) is the average of the deviation of the real policy rate (r[k]) from r*[k], for the previous two time periods multiplied by -0.608. This formulation means that an interest rate shock has an effect on the output gap both one and two quarters later. Interest rate settings would normally be assumed to be the result of some Taylor Rule. Normally, we could expect the effect of interest rates to be aimed to drive the output gap to zero, but it could conceivable go the other way if the central bank is trying to drive inflation back to target. Since I want to abstract away from inflation and interest rate dynamics, we will see what happens if v[k] is zero. 

This leaves us with the external disturbance. Since the system is linear, we can decompose the dynamics into being the sum of two trajectories.

1. The effect of the disturbance where the system starts with at equilibrium.
2. The effect of starting away from equilibrium, with no external disturbance.

If the internal dynamics of the system are stable, the first component -- the effect of the external disturbance -- has the property that the output has a bounded magnitude relative to the input. (We use the concept of a mathematical norm of a time series to assign a magnitude to its "size.") That is, in order to get a "large" output of the system (in this case, the output gap), we need a "large" disturbance signal. This is because the system stability implies that the system state will return to its equilibrium (zero output gap) if the disturbance ceases.

Stability Analysis

We still need to verify that the system is stable. One initial test is to simulate the response after starting at a non-zero initial condition. (This is not enough formally to validate stability, but if the trajectory does not explode, the odds are good that it is stable.) The above figure shows the output gap simulation that results after one initial condition and no disturbances (interest rate policy or external disturbances). Since the output gap depends upon its value from two time periods previous, the first two values of the output gap represent the initial state that needs to be set before the calculation can go forward.

As can be seen, the output gap decays to zero. This matches a formal stability analysis, which looks at the properties of the matrix that defines the dynamics. (We look at what are known as the eignevalues of the matrix. The eigenvalues are 0.775 +/- 0.09i, where i = square root of -1. This is a pair of complex numbers, which have a modulus less than 1. This meets the requirement of being a stable discrete time system.)

The system dynamic equation looks a bit strange, why are the coefficients for the two lag terms of a different sign? The reason is that this configuration gives rise to some extra oscillatory dynamics (as evidenced by the complex eigenvalues). This explains why the output gap has a small rise in the third time period relative to the initial conditions level before moving towards a steady decay dynamic.

Recession Awkwardness

The concern with using stable models is that recession dynamics represent a problem. In the absence of a shock (or a central bank that deliberately destabilises the economy), the output gap will track around zeros. If we allow for a sequence of small shocks that are of varying signs, we will just get a small noise signal around data (which is reasonable for during an expansion).

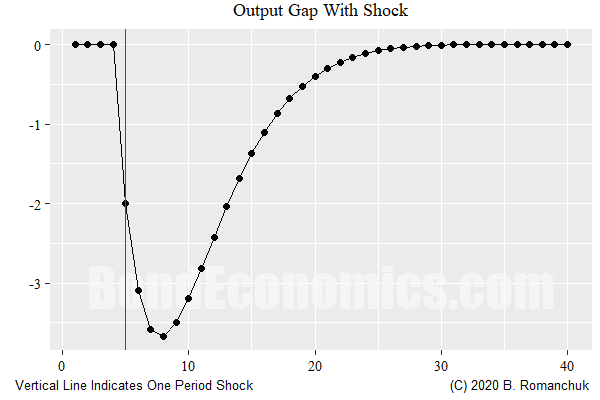
In order to reproduce the behaviour of recessions -- infrequent plunges in activity -- we need a larger shock. The figure above shows the result of a single shock that occurs at t=5. The system dynamics magnify the initial shock, then the output gap decays. The decay is relatively slow, but remember that I have set the effect of monetary policy to be zero -- normally central bank actions would result in a more rapid stabilisation within the model. Since the central bank action enters with a lag, it would not be able to stop of the initial negative overshoot, rather it can only speed up the decay.

This gives us a few empirical issues when applying the model.

• We cannot really say why the recession happened. Although the shocks within the linearisation are supposed to changes to preferences or productivity, we have lost information when we linearise. Since there are an infinite number of nonlinear models that give rise to the same linearisation, there are any number of potential culprits to generate "shocks."
• The shocks are random, and so cannot be predicted. This has some similarities to my view that recessions are hard to forecast. However, my arguments follow from arguments about the structure of the economy, not that outcomes are just a dice roll.
• The shocks are asymmetric, with no extremely large positive growth shocks mirroring recessions. Standard estimation techniques assume symmetry, and so recessions end up being coincident with drops in r*, That is, the deviation in GDP is seen as being improbably large, so the estimation technique has to put some weight on the possibility of interest rate policy causing the economy to contract (which happens if r* drops below r.) 
• Once we factor in the effect of monetary policy, recovery from recessions should be quite rapid, which has not been the case in the post-1990 era.
• It is not obvious why a shock in the past should have such a large effect in models that assume rational expectations. This calls into question the relationship between nonlinear DSGE models and linearisations fitted to data.

At this point, evaluating the models appears entirely subjective. If one is happy with the argument that recessions are just bad die rolls, one can stick with standard DSGE macro. Otherwise, there needs to be some structural changes made to the model. The question is: can those new models be fit to data?

Note that my comments here are somewhat preliminary, and will be digging into the subject deeper later in the writing process. However, they do appear to outline the fundamental issues that discussed in more opaque terms in the academic literature.

(c) Brian Romanchuk 2020