The Perils Of Non-Causal Models: r* Edition

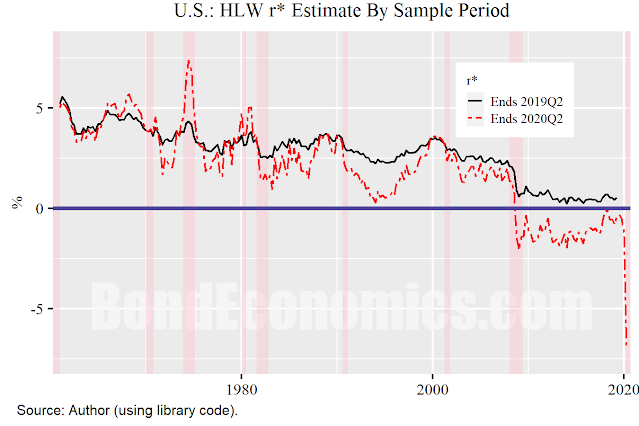
One important property of time series is models is whether they are causal or non-causal. A non-causal model has the property that future values of inputs affects the current values of outputs. For time series, the calculation implies the use of a time machine, which is generally not available. One needs to be careful of the issues posed by non-causality in financial model building, since time series libraries treat time series as single units, and contain many non-causal operations. However, as I discovered the hard way, the Holsten-Laubach-Williams (HLW) model is non-causal, and the 2020 spike causes some serious issues (figure above). I previously analysed the model, but had not realised the magnitude of the problem associated with 2020. Although my qualitative analysis was not greatly affected, the charts were perhaps too sensationalistic. 

The chart shows the effect of adding one year's worth of data to the model fitting, that is, extending the sample period from 2019Q2 to 2020Q2. The volatility spike in 2020 blows out the volatility estimates, and disrupts the fit. (The volatility issue was pointed out to me in online correspondence.)

The problems with non-causality are readily apparent in this example. The value of r* is much more volatile, and dropped to a negative value in the past decade. This gives us a different perspective on the post-Financial Crisis period than what we would have said just one year earlier. 

The New York Fed r* website has new versions of the algorithms that incorporates a dummy variable that counters the 2020 effect. From my perspective, this takes an already complex algorithm and adds yet another level of complexity. It also raises the issue that the dummy variable is to a certain extent arbitrary, and so the output can be controlled via the dummy variable. Different people can choose different dummy specifications, and get different outcomes.

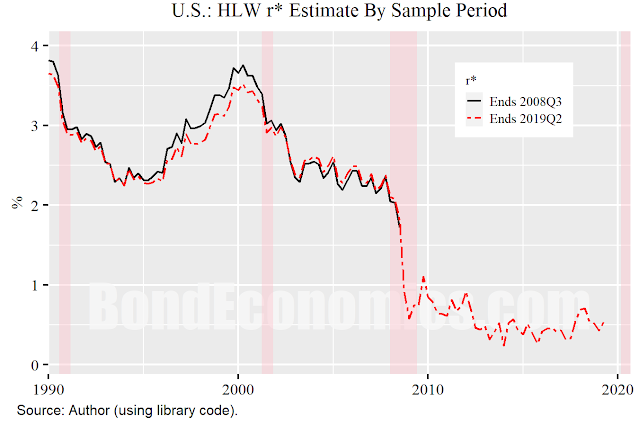
It should be noted that 2020 stands out here, the 2008 recession does not have the same effect on the fitting (figure above). There is a small revision to the r* estimate before the year 2000, but that is about it. I knew the algorithm was non-causal (I noted it in the previous article), but underestimated the 2020 impact, assuming it would be similar to the 2008 effect shown above. The issue is that the model assumes a normal distribution for disturbances, and thus is too jumpy with respect to outliers, since the normal distribution has thin tails.

Solutions for Non-Causality

There are two standard ways of dealing with non-causality in financial modelling, involving the use of the concepts of windows.

1. A moving window, which recalculates the estimate based on the last N years of data. 
2. A stretching window, which recalculates the estimate using the entire data set each period.

Neither of these methods would be very helpful in this case. A stretching window will be disrupted for an extremely long time, perhaps another century. A moving window would eventually recover, but this methodology needs a fairly long window, so that might still take 50 years.

Another method would be to freeze the estimated model parameters based on a long history (e.g., ending 2019). The model would then just consist of a Kalman filter attempting to infer the hidden state variables for that fixed model. This is the simplest solution, and would align with engineering practice. 

Alternatively, one could switch to a methodology that is not sensitive to outliers in the data. That would be a desirable property in engineering or financial modelling. However, it might require rebuilding the entire statistical methodology from scratch. Although that is probably what I would do, there is no guarantee of success. Furthermore, the odds are that more robust methods would rely on sub-optimal heuristics, which is extremely unpopular within the mainstream academic community, which demands optimal solutions whenever possible.

(c) Brian Romanchuk 2020