This article outlines my initial results of running the Holsten-Laubach-Williams (HLW) model that generates an r* estimate. The New York Fed page describes this and the Laubach-Williams (LW)model: https://www.newyorkfed.org/research/policy/rstar. The New York Fed page offers replication code, in the R language. The Laubach-Williams code failed for me, and I ended up finding a GitHub repository with code for the HLW model by Jannes Reddig: https://github.com/JannesRed/rStar.
Note: I have discovered the hard way that the estimation procedure is sensitive to outliers, in particular the 2020 collapse in GDP. Although it has a dramatic effect in the charts here, it had an effect that I did not expect -- it impaired the parameter estimates. The r* estimates shown here are much lower in the post-2009 period than they were in estimates that used data that ended in 2019 (e.g., as shown on the NY Fed website). I have replaced some of the charts with data sets ending in 2019.
Since I had been spending my time looking at other r* estimation models, I will not give a lengthy explanation of the model. This article represents initial experimentation, and the model is behaving in a way that I expected, based on first principles. (This work will be developed and put into a chapter in the second volume of Recessions.) Although I will outline my big picture concerns about the methodology, I will keep my discussion tentative.
Model Outline
The HLW model is a somewhat simplified version of the LW model, making it easier to apply to other countries. (The New York Fed page shows other countries, I am just looking at the U.S. data since the narrative around it is familiar,)
Importantly, the model is an empirical model, designed to be fit to data. It is supposed to be interpreted as the linearisation of a nonlinear New Keynesian model, but this desired interpretation does not take into account that there are an infinite number of nonlinear models that give rise to the same linearisation. As such, there is no need to worry about all the complex optimisation problems etc. that are allegedly features of mainstream macro model; it is a simple discrete time model generated by a complex econometric procedure.
The model determines r* by setting it to be the sum of two factors: trend real GDP growth, and other factors. (This decomposition is simpler than the LW model.) Since the construction implies that two of the variables implies the third, we can think of the model as determining two hidden state variables: trend GDP and r*. The use of trend GDP means that the output gap (difference of actual GDP from trend) is important for inflation (and not the equivalent of NAIRU).
The inputs to the model are as follows.
- Log real GDP.
- Inflation (core PCE).
- Inflation expectations - which is an adaptive expectations measure (!) based on core PCE.
- Fed Funds rate (nominal).
The real rate used in the model is the nominal Fed Funds rate less the adaptive expectations inflation measure.
Results On Historical Data
 |
| (Sample: going to 2020.) |
The figure above shows the real Fed Funds rate and the r* estimate. As can be seen, r* fell to a negative level in the past decade, making it allegedly impossible to stimulate the economy with interest rate policy (since the nominal rate was stuck at the zero lower bound).
One eye-catching observation is that the r* estimate plunges at the latest data point -- the COVID recession. This is our first clue that the actual construction of r* does not align with the textual discussions of its properties.
Deep Recessions Cause r* to Fall by Construction
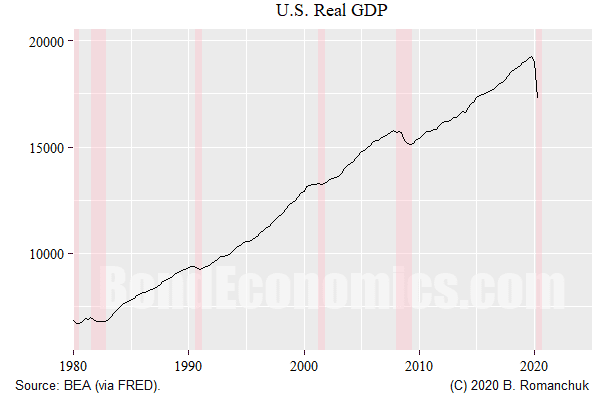
We need to put aside narrative theories about r*, and look at the algorithm construction to understand its behaviour. The estimation econometrics assumes that deviations to behaviour are convenient random variables that are symmetric. If we look at the above chart of real GDP, that sort-of seems plausible -- during expansions. During the last two downturns, there were dramatic plunges in real GDP in short periods of time. There are no similar upward jumps to be seen.Since the model is attempting explain the evolution of (log) real GDP by the deviation of the policy rate from r*, if the assumed random shocks cannot do the job, r* has to move. Since GDP falls, that means that the policy rate is allegedly too high relative to r* -- and so r* drops like a rock.
In order to believe the model, we need to accept one of the two possibilities:
- the recession in 2020 was caused by a plunge in r*, or
- r* falls because we had a recession.
Since neither possibility appears plausible, new versions of the models have been released on the N.Y. Fed webpage, with a dummy variable used to notch out the 2020 recession.
The question then arises: why notch out just the 2020 recession, and not the Financial Crisis, where exactly the same dynamic occurred, just in a less implausible format? (UPDATE: The causality issued I discovered after writing this article probably explains this disparity.)
Counter-Factual Analysis
In order to properly test an applied mathematical model, we need to look at how robust the model is to model specification error. Mainstream economists still rely heavily on 1960s optimal control theory, but they have not come to terms with the reasons why control engineers abandoned almost all of optimal control theory (outside the Kalman filter and path-planning applications). Parameter uncertainty -- which economists look at -- is not model uncertainty, where dynamics are different than assumed. (In engineering, a small time delay in the response is all that is needed to turn an optimal control rule into a death trap, while the optimal control rule will be impervious to reasonable deviations in parameter values in the original model.)
To do robustness analysis, we need to test the model behaviour on data generated by different dynamics. For reasons that will be clarified in a later article, I am looking at a counter-factual scenario, one where interest rates are shocked higher after 2010, by either 200 or 400 basis points. (The figure above shows the 400 basis point shock.) No other input variables are changed.
The shock motivation is straightforward: what happens if the economy is not sensitive to interest rate movements? How does the model react?
 |
| Sample end: 2019Q2 |
The figure above shows the new estimate of r* and r. The estimate of r* plunges courtesy of the Financial Crisis recession, then tracks toward the counter-factual level of r. (Note that this figure is based on a sample ending in 2019Q2.)
 |
| Sample ends in 2019Q2 |
The above figure shows the step response of a 200 and 400 basis point shocks to the nominal rate. Instead of showing the levels of the variables, the differential between the scenario and the historical fitting is shown.
The r* estimate lies on top of the original almost exactly until the shock, with the small deviations before 2010 being the result of the model parameter estimates being based on the entire data set, thus making the overall model non-causal (changes to future data modifying the current output). Once the shock hits, the r* estimate in the shocked scenarios decays towards the new shocked level of r*, and we can eyeball the charts to see that the decay rate is just under 50% of the shock level per decade. (The decay was faster in the version of the model that included the 2020 outlier, being about 75% in a decade.)
Why r* Fell
Demographics (or whatever factor people are sticking into dual y-axis charts) has not called r* estimates to fall since the Financial Crisis. It is a result of two properties of the construction.
- Deep recessions represent an asymmetric shock to real GDP, and they cause an immediate downward shock to the r* estimate, which takes a long time to decay.
- The r* estimate will always decay towards the observed level of r if the economy reaches a pace of steady growth of inflation -- which has always been the case in post-1990s expansions. The value of r* is low because New Keynesian central bankers have planted r at a low level.
Technical Appendix: Falsifiability
My shock scenarios were not an arbitrary choice, although they were useful for this article. They are part of a longer argument: what happens if we apply neoclassical econometric techniques to a model where interest rates are ineffective in steering the economy?
What happens is that the estimation procedures will always find a r* estimate, and that r* estimate will always suggest that the policy rate is just in the wrong place. If r allegedly moved, then outcomes would be different. However, if we apply that counterfactual to the model that suggests interest rate ineffectiveness, there new r* estimate will just move, and so we would need a counter-counterfactual scenario.
In other words, the methodology cannot distinguish between models where interest rates are effective in steering the economy, and ones that there is no effect.
Given the importance of "star variables" (r*, g*, u*) in neoclassical economics, results like this are extremely troubling if we want to fit them to data -- which is allegedly the reason why we need complicated mathematical models of the economy in the first place.
(I will be writing this argument out in full in later articles, once I have covered the basic theory more thoroughly.)


Hey Brian, it’s Chris, haven’t talked in forever. That NK models output really simple hidden state machines is something I learned from Shalizi a long time ago (probably in Almost None Of The Theory Of Stochastic Processes somewhere). This feels like a model that takes three inputs and gives three outputs but kind of pretends to have four to make it seem like some thought was put into the psychology of prediction or somesuch.
ReplyDeleteIf I am misunderstanding this problem, then let me know and have a great day!