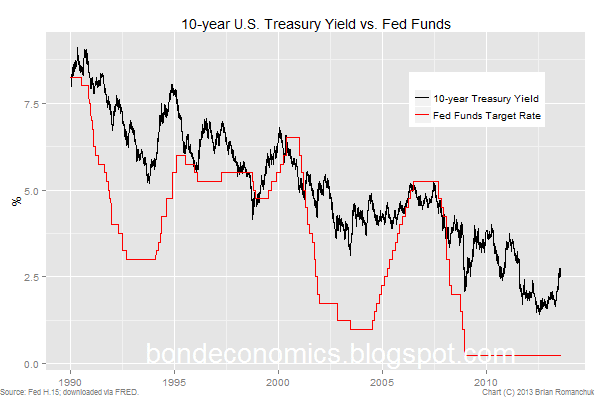
A major topic of interest of this blog is interest rate formation – what are the factor(s) that determine bond yields over time? In other words, how can we model the squiggly line in the chart below? Note that throughout this article, I am referring only to (central) government bonds that are issued in the local currency. For example, pricing a corporate bond needs to incorporate a premium to cover the risk of default. (NOTE: this article is an introduction to this the subject; see this "Theme" post to see further discussion of this subject.)
My response, which I believe is non-controversial amongst most bond market practitioners, is that interest rate expectations are the primary explanation for the level of yields. (The preferred formulation of a portfolio manager I worked with was “interest rate expectations with technical factors”). In fact, this view is so non-controversial I would guess that many will have stopped reading already (“Well, duh! Time to go back to reading TOP on Bloomberg.”). For those of you who have continued reading, I want to cover some of the less obvious implications of this viewpoint.
One simple formulation of the interest rate expectations
model is: the yield on a (credit risk
free) bond should equal the expected cost of financing the bond at a short-term
rate over the bond's lifetime.
This essentially is a statement that the bond market is efficient. The initial yield to maturity
of a bond represents the breakeven point of the strategy of buying the bond
with 100% leverage and holding it to maturity. If we take a 10-year bond* as an
example, the implication is that the yield should equal the expected (geometric)
average of the 1-day financing rate over the next 10 years**.
One should also slap a risk
premium into the bond yield, but the assumption here is that this risk premium should be small and stable; for example running around 25-50 basis points or so.
In the U.S. Treasury market, the
cost of financing a bond overnight (the overnight repo rate) is typically close
to the Fed Funds rate, which is supposed to be near the Fed Funds Target Rate set
by the Fed. There can be spreads in those funding costs, but they are of the
magnitude of dozens of basis points, which is a small residual relative to the
volatility in the pricing of most Treasurys with maturities two years and up. Therefore, it is not an accident that there
appears to be some sort of relationship between the “market-determined”
10-year yield and the “administered” overnight rate (Fed Funds Target in the
U.S.).
What I find interesting about this point of view are the
things that do not directly determine
the level of bond yields. Examples:
·
pretty well every fiscal variable (deficits,
debt/GDP ratios, whatever);
·
what big investors (e.g. Chinese reserve
managers) are doing;
·
the size of the central bank’s balance sheet
(QE!);
·
inflation (but see note below);
·
expected returns for other, lesser, asset
classes like equities;
·
the level of real rates versus some benchmark
level such as an historical average or zero;
· bond yields in other
currencies;
·
how the currency is trading.
What may be a surprising theme is that supply and demand don’t matter (e.g. deficits or investor
positioning), rather the assumption is that markets are efficient discounting
mechanisms for expected returns***. Unusually,
“free market oriented” economists, who are typically associated with holding a
“markets are efficient” view can quite often write commentary implying the
opposite – that fiscal variables can have a major impact on the bond yields
(for example).
However, the unanswered question is: what determines the
expectations for the short-term rate? In the absence of reliable crystal balls,
market participants are stuck with attempting to model the central bank’s
reaction function. Thus, inflation is only an indirect input to the “model” for
bond yields - it only matters if the central bank reacts to it. Of course,
since most relevant central banks practice inflation targeting, it should be a
relatively important input, but as I will discuss in future posts, observed inflation
has not been very relevant in practice for the last 20 years or so.
* In the U.S. market, Treasurys with 10-year maturities at
issue are officially referred to as “Treasury Notes”, only longer maturities
like the 30-year are “Treasury Bonds”. However, I used the generic “10-year
bond” (lowercase) for simplicity.
** You need to correct for the various archaic yield
conventions used in the bond and money markets if you want to get all fussy about the calculations.
***Supply and demand represent the “technical factors”
alluded to in the quote by the portfolio manager above. I feel that these
factors are mainly visible in maturities beyond the 10-year point, e.g.,
30-year bonds. Even so, the magnitude of these factors are generally quite small, other than for some extremely distorted markets like the gilt market after various pension reforms in the 1990s.
(c) Brian Romanchuk 2013

As you say the role of expected future short rates is pretty uncontroversial here. However, I do not entirely agree with the dismissal of the of the risk premium as small and stable. This is where the supply and demand come in. For a start, the appropriate level for the risk premium depends on the investor. Households might see longer dated bonds as carrying more duration risk, whereas pension funds might see them as less risky because they are a better match for their liabilities. The level of perceived risk on an asset also depends on how it fits with the rest of the investor's portfolio - if you're already 100% in bonds, then another bonds will feel more risky than if you're 100% in equity.
ReplyDeleteThese things all depend on supply and demand and will be impacted by many of the things you list under the 2nd graph. Quite how important they are is difficult to gauge, although I agree they will be less relevant at 10 years than in longer maturities. My own feeling is that, whilst they are not as important as short rate expectations, they are still material.
To be honest, my views are somewhat more complex, but "complex" can also be read as muddled. I have to avoid burying my points under a sludge of special cases (which is my natural tendency). The "supply and demand" question is fairly complex, which will be fodder for future articles.
DeleteThe "small and steady risk premium" text is a hook that will turn into a link to a planned future post. I dislike a lot of the models coming out of academia for yield curves where pretty much all the volatility is explained by shifting risk premia. This sort of model behaviour makes no sense to me, for reasons I will explain in the future (yay, more material).
This comment has been removed by a blog administrator.
ReplyDeleteThis comment has been removed by a blog administrator.
ReplyDeleteBrian, long time no talk. Have you ever done a study to see if the Stone McCarthy Duration Manager's Survey has any information with regards to the future direction of interest rates? Does a survey that tells us bond managers are short duration suggest a contrarian play on the direction of yields?
ReplyDeleteHi - yes it has been awhile. I don't have access to that data, so I have not done a study of it. I used to have access to it or another duration survey, and I think it sort of worked as a contrarian indicator at extremes. You could pick out those extremes after the fact visually, but to identify those points in real time was the real trick. I am still trying to add data sources over time, and I probably will add the CFTC positions data. I could then see if there's anything I can do with that.
ReplyDeleteA few points:
ReplyDelete(1) The expectations hypothesis gets little or no empirical support. There's a large body of research looking for evidence that current long rates convey information about future short rates, and the results are overwhelmingly negative.
(2) The expectations hypothesis does not necessarily describe the behavior of rational investors even in principle. In general, if you expect the price of a long bond one year from now to be X, then the price you should be willing to pay for the bond today will be close to X, no matter what path you expect short rates to follow. That's because if there is a significant change in long rates, the resulting capital gain or loss will swamp the yield in total return. (This is more true the longer the maturity of the bond, and the lower are current rates.) The main concern for someone buying a long bond today is the future path of *long* rates, not short rates. So if market participants believe for whatever reason in a stable long-term level of long rates, then within some limits that belief will tend to validating (i.e. rational investors will have no reason to depart from it), regardless of their beliefs about future short short rates.
(3) Liquidity matters, even when we are just talking about Treasuries of different maturities.
I probably should look a bit more at the literature. I did my analysis working directly with the financial data and testing out trading ideas. I ran into very little academic literature that was useful for doing my job. (Obviously, market practitioners are paid on the view that markets are not perfectly efficient...) Now that I am writing here, I probably need to pay more attention to the literature.
Delete(1) I am willing to accept that the bond markets can do a bad job of predicting the future. But I would argue that forward rates are close to what bond market participants expect (perhaps not economists as measured by surveys, as surveys have a groupthink bias and lag the markets). There is the issue of the term premium, as well. One could argue that my description is tautological, but it is still useful as a starting point.
I would note that "physical" bonds - for example, particular Treasury issues - can depart from nice clean forward curves for a number of reasons. Swap curves do not have those problems.
(2) Yes, if your holding period is 1 year, for a 10-year bond (swap) you are interested in the 9-year bond, 1 year from now. But what determines that future 9 year rate? Ultimately, it is the path of expected short rates for 9 years.
I recognise that "expectations" as an explanation breaks down starting around the 5 year point, at which point "convention" takes over. Even so, those conventions are kept in line by forward rate behaviour.
(3) I am in the process of writing about liquidity (which complements your recent article); the article should be out this weekend.
But with regards to the Treasury curve, yes bond deviate from a clean curve. Which is partially the result of differences in repo rates; benchmark notes and bonds are not as expensive as they look when you look at yields, as they typically fund at a cheaper rate ("on special") in the repo market. Since getting that repo rate information is difficult, I would stick with swap rates,
Yes, if your holding period is 1 year, for a 10-year bond (swap) you are interested in the 9-year bond, 1 year from now. But what determines that future 9 year rate? Ultimately, it is the path of expected short rates for 9 years.
DeleteWell, that's one hypothesis. But it need not be true as a matter of logic. It is perfectly possible for me to believe that the short rate will be 3% and the 10-year rate will be 6%, for the indefinite future. If you look at the data over the last 30 years, there is in fact a fairly stable 3 point gap between 10-year yields and the ex post average short rate over the life of the bond. Now, it is possible that investors have consistently overestimated the future level of short rates over the past 30 years. But if the markets can be systematically wrong about future short rates, then I as a rational investor should be thinking more about the expectations of short rates embodied in long rates, than in what short rates will actually be.
You are a professional in this area, I'm anything but. But it's certainly my impression that bond market participants do hold definite beliefs about "normal" or "reasonable" levels of long rates, that are at least somewhat independent of what they expect the Fed to do.
DeleteAnd people like Alan Greenspan have argued that international arbitrage between long bonds is becoming more important relative to arbitrage between different maturities in the same currency, which would again weaken the expectations hypothesis.
Yes, you need to embed what you think the market thinks the term premium should be.
DeleteHowever, I believe that the persistence observed term premium is the result of auto-correlated missed forecasts. Nobody believed that short rates could sustainably at zero for years, even with the Japanese yield data easily downloaded. I would argue that it makes no sense to put a 3% term premium on a 10-year bond when the market struggles to keep investment grade spreads near 100 basis points.
And if you are an investor that thinks you can do short-term market timing, you are worried about what the long-term rate will be 3 months from now. There are tons of market models that purport to do just that. I am unconvinced that any of those market timing techniques work, which is why I look at intermediate-term rate expectations. There is an investment philosophy behind my discussion, which I will sooner or later write down.
(Note: my previous response was with respect to your earlier comment; the order of comments are being mangled.)
Delete"You are a professional in this area, I'm anything but. But it's certainly my impression that bond market participants do hold definite beliefs about "normal" or "reasonable" levels of long rates, that are at least somewhat independent of what they expect the Fed to do."
I have seen a lot of crazy theories about interest rates from market participants, to a certain extent my relatively fundamentalist expectations view developed in reaction to that. Obviously, people can disagree with my views. But it is a good starting point, even if people want to debate about things like the term premium.
Most dedicated fixed income people will look at long-dated forwards, such as the 5-year rate, 5 years forward. That is largely beyond any reasonable forecast horizon for the path of short rates, and represents an average expected rate level (plus term premium). Non-specialists tend to ignore forward rates, and they tend to generate comical yield forecasts as a result. (Bank fixed income strategists often wince when they have to give their chief economist's yield forecast.)
"And people like Alan Greenspan have argued that international arbitrage between long bonds is becoming more important relative to arbitrage between different maturities in the same currency, which would again weaken the expectations hypothesis."
Outside of emerging markets, I don't give this theory much credence. All the major private fixed income investors live in a world where they cannot take foreign exchange risk. FX is another department. (In EM, nobody hedges currencies.)
The only people who can take FX risk like that on "bond" positions are a handful of macro funds - who have tiny balance sheets, and central banks. Central banks manage their FX exposure based on a number of constraints, plus they tend not to take wild duration risk.
On a one year horizon, an unhedged cross currency spread trade would have a forex risk that dwarfs the interest rate spread risk. A spread could move about 100 basis points, which translates into about 7-8% return risk. Currencies can run 20-30% against you on that kind of a horizon. On a longer horizon, it starts to make more sense, as spreads compound, and currencies revert to "fair value". For example, I previously bought U.S. Treasurys on long-term valuation grounds (I'm Canadian), but my personal portfolio is not going to move the market...
Thanks for the responses. This is extremely interesting!
ReplyDeleteSo you would say that uncovered interest parity is nonsense, then?
Yes, the forex and interest rate markets are independent. Interest rate parity - the fact that interest rate differentials (PLUS the "basis"*) holds in the sense of the determination of where the forwards trade relative to spot. If people are selling a currency forward, then that will drive down spot, rather than impact interest rate differentials
DeleteSince interest rates in the different currencies are independent, this means that forward currency levels will not have any predictive value for future currency rates (which is what the literature finds, I believe).
Obviously, things were different in the Gold Standard, or other forms of managed currencies. In those cases, bond spreads become a means to speculate on potential changes to gold parities.
* The currency basis markets started to wobble during the financial crisis, and that got central banks' attention in a hurry. It is the most important market nobody has heard of.