Note: This is an unedited draft from my inflation primer manuscript.
The creation of price indices is not an easy task and involves many steps. Furthermore, each major index is different – different countries have somewhat different methodologies, and a single country will typically have multiple price indices that have different methodologies.
Statistical agencies typically have a lot of information on the methodology behind consumer price index calculations. Given the popularity – and controversy – associated with these indices, they offer explanations at different levels of required background knowledge. The technical explanations typically just explain the methodology used, and that should be easily followed by anyone with mathematical training. The complex part of price indices is choosing the calculation methodology, which might require dipping into the technical literature. However, for those of us who are not creating our own price indices, that level of detail is normally not needed.
There are three main steps needed to calculate a consumer price index.
- Determine weightings based on consumption.
- Go out and measure prices in the economy.
- Aggregate the measured prices into sub-indices which are in turn aggregated into an overall price index.
1. Get Weights
The real world is complicated and not all prices change by the same percentage amount each month. We need to assign a weighting to prices to see how much they contribute to the overall (sub-)index movement. In order to be compatible with the way that price indices are used in economic theory, the weighting should reflect the quantity of items purchased in a period. That is, if 5% of spending in the month was on gasoline, gasoline prices get a 5% weighting in the inflation reading.
However, the government does not monitor all transactions in the economy (yet…). We do not know the exact amounts of all purchases, and so we need to estimate them.
The estimates of consumption weighting will be based on surveys of consumers from previous years. The Bureau of Labor Statistics (BLS) in the United States summarises its methodology as follows (https://www.bls.gov/cpi/questions-and-answers.htm):
For example, CPI data in 2020 and 2021 was based on data collected from the Consumer Expenditure Surveys for 2017 and 2018. In each of those years, about 24,000 consumers from around the country provided information each quarter on their spending habits in the interview survey. To collect information on frequently purchased items, such as food and personal care products, another 12,000 consumers in each of these years kept diaries listing everything they bought during a 2-week period. Over the 2 year period, then, expenditure information came from approximately 24,000 weekly diaries and 48,000 quarterly interviews used to determine the importance, or weight, of the item categories in the CPI index structure.
A key point is that the weighting is determined with a considerable lag. This causes problems in the calculation step of the process.
2. Measure Prices
On the previously linked page from the BLS gives an overview of the price sampling process. They claim to process 80,000 prices in a sample each month.
The easiest-to-understand method of determining the price is when workers at the agency sample particular prices at shops or websites. Ideally, the worker goes to retailer and looks for a specific item – e.g., 12 large eggs. The price is then recorded and can be compared to the previous month.
However, firms change around their products. The size of a cereal box might change. In that case, the worker will find the best substitute for the target product (using pre-determined rules), and then the price for the substitute product and its details are submitted. The statistical agency will then make an adjustment to allow the price sample to be used.
For example, a statistical agency might adjust the price to take into account a change in weight of the contents of a cereal box. If the new box has 10% less cereal, the old price would also be adjusted down by 10% to match to the current price.
Since consumers dislike price changes, shrinking products is one way to disguise price hikes – typically called “shrinkflation.” Although this might be enough to mislead consumers, statistical agencies have been aware of this tactic for decades, and the survey methodology takes it into account.
However, not all goods and services are bought in stores at advertised prices. Other items in price indices are more complicated to deal with, and prices are measured in different ways. Rents are a large expenditure category, and are typically tracked by longer-term rent surveys. Since rents on particular dwellings are typically adjusted on an annual basis, the associated price index ends up being smoothed over time.
In some cases, “prices” are calculated based on models, and not measured prices. These “imputed” prices tend to show up more in indices mainly used by economists like a GDP deflator, and not consumer price indices (which are used in contracts).
3. Index Calculation
The last step in creating an index is to move from measured prices (after any adjustments) towards an index. Although a very simple price index could consist of an average price of some generic items that are fixed over time, this will not work for the price indices calculated in economics. Instead, the idea is that the index experiences a percentage change in a month that is in some sense an “weighted average” of the percentage change of its components.
The problem for index calculation is that statistical agencies do not have a live update of weights for the consumption basket. They have weightings that are calculated based on a survey that was taken years earlier.
To give a simplified example of the issues, imagine a convenient economy where apples and oranges were the only fruits available, and they both sold for $1 a piece for a multi-year period. The survey indicated that consumers purchased 10 apples and 10 oranges monthly (for a total expenditure of $20).
Then, the Lack of Rhyming Virus hit orange producers, and orange prices doubled in one month, with apple prices unchanged. Given a 50/50 weighting, the monthly inflation rate is 50%, which matched the 50% increase in the cost of buying 10 apples and 10 oranges ($30, versus $20).
What happens if orange prices double again in the next month? That would be another 50% monthly inflation rate if a 50/50 weighting is maintained. The problem is as follows: what happens if consumers decide they do not want to buy really expensive oranges? In fact, since the reason for the price spike was a shortage of oranges, it was literally impossible for consumers in aggregate to buy as many oranges as before.
In the most extreme case of substitution, consumers would stop buying oranges completely, and just buy 20 apples – at an unchanged cost of $20. That is, there is a 0% inflation rate, rather than two months of 50% (cumulative inflation of 125%). Although this is a rather extreme made-up example, we can see that substitution will affect the calculated inflation rate.
Since statisticians do not have access to the information on every single transaction in the economy, they need to use a model to estimate how much substitution happens in response to price changes. This model then determines the weighting scheme for updating a price index in response to price changes in its components. Since I have no particular expertise in that area, I will let any readers interested in the topic to go to the resources at the national statistical agencies. The formulae are ugly but are not truly complicated if you are familiar with mathematical notation.
The fact that assumed substitution reduces measured inflation generates considerable popular anger. Anything that reduces inflation is seen as a conspiracy by government statisticians. If the objective were to measure the cost of purchasing a fixed set of goods forever, this complaint would have legs. However, the objective is to measure the trend in prices in a capitalist economy, and consumers’ basket of purchases changes over time. The entertaining part of the complaints about substitution typically come from rabid fans of the free market – and one of the selling points of the free market is that it provides price signals that guide behaviour.
The effects of substitution in a given month are much smaller than my made-up example. However, even a small effect on a monthly basis will accumulate to a large difference on a multi-decade horizon – which is often how price indices are used. Choosing the methodology to maximise the inflation rate each month to keep the inflation nutters happy would result in an inflation index that greatly overstates the inflation rates of actually purchased goods and services, and this would distort economic statistics. In any event, the accumulation of uncertainty as a result of this effect is one factor leading to my skepticism about the comparability of price indices over long stretches of time.
Quality Adjustment
A final area of theoretical dispute in price measurement is the question of quality adjustment. As noted earlier, it is easy to adjust for changes to the size/weight of sold products – but what about changing quality? One popular pastime among oldsters (like myself) is complaining about everything going to pot.
To the extent that adjustment for quality is possible, it needs to be turned into a quantitative adjustment. We could imagine that if a new model of car has a longer expected operating lifespan than the previous generation, we could compare its price to the previous generation on a dollars per expected operating lifetime basis.
For most products, I am unconvinced about the importance of this effect. On a horizon of a decade or more, there would be serious “positive and negative quality gaps” for different products – which is yet another reason to take long-dated price index changes with a grain of salt. That said, there were products that generated considerable historical controversy – computers.
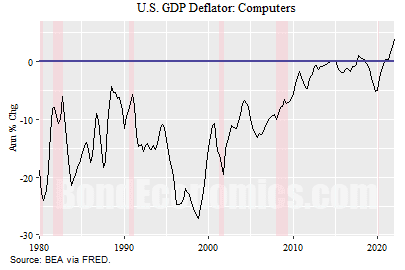
The previous figure shows the annual percentage change in the GDP deflator for computers. (The price index used in GDP calculations is referred to as a deflator.) If you focus on the late 1990s – when the controversy got serious – we see that the deflator was falling over 20% per year. What this meant that if the nominal spending was unchanged, a 20% drop in the deflator would imply that real spending (i.e.. inflation adjusted) grew by 20%. Although computer spending was not a huge weight of overall GDP, this represents a significant magnification.
From a user standpoint, it was not clear that prices were falling to that extent. In the late 1990s, I went desktop computer shopping a few times on a somewhat regular basis (for myself, and family). You would see a range of models, but all the interesting ones were in a fairly tight price range. (This was different than today, where there are a lot of price points for desktops and laptops.) Each time, the computer with the best price/capability trade-off from my perspective was pretty close to $1000 (Canadian).
This was not a magical coincidence. In the tech industry, products aimed at retail are typically sold at target price points. The nominal price of video game consoles and the latest hit video games (sold in stores) have not changed that much since the late 1970s. For computers and game consoles, there is a target price, and components chosen to hit that price.
The reason why the deflator was falling was that each year, the new computers were more powerful – more memory, larger hard drives, more computing cycles from the processors. That is, the deflator was falling because of quality improvements, and the quality improvements were measured based on the quantitative metrics.
European economists – particularly Germanic economists – were outraged by this situation. They argued that statisticians in the United States were cooking the books, flattering American GDP growth rates versus the European GDP growth rates, as the European GDP deflator was not falling as rapidly. Given that some Austrian economists were in fact of Austrian descent, this drama made its way into Austrian financial/economic newsletters as well as the fledgeling “economic bear website” discourse. Since statisticians referred to quality adjustments as “hedonic adjustments,” one encountered a lot of raging about “hedonics.” (Hedonic comes from the Greek word for pleasure, and quality adjustments were based on the “utility” of the changes, and “pleasure” was used as a synonym for “utility.”)
This argument has faded from view, mainly because the deflator has largely calmed down. (There was also the issue that some of the European critics misunderstood how GDP calculations worked, and their estimates of the effect of quality changes on real GDP growth were wildly overstated.) As such, one will not hear much about this effect in “mainstream” economic discussion. However, memories have not completely faded within the Austrian community, and so one still hears random rants about “quality adjustment” to this day on the internet.
Although I am not incredibly sympathetic to popular Austrian economists, I do have sympathy for the argument that the deflation in the computer deflator was misleading (although the alleged effect on real GDP was a red herring). Most (well written) modern software that interact with users does not utilise much computing resources; the processors are mainly idle and waiting for user inputs. As such, an increase in computing power does not affect the usage of the computer for a great many purposes. (The main exceptions will be server clusters, heavy computational tasks, and high-end action video games.) I bought a desktop computer in grad school in 1993, and I use it pretty much the same way I use my computer now: I sit in my pyjamas, drink coffee, type on a keyboard, and characters appear on the screen. From a writing perspective, the advances increased computing power have allowed for features to increase productivity, but the increases are less dramatic than the increase in computations per second suggest.
Readers interested in further details on the effect of computer deflation on growth rates, Paul Schreyer wrote an article discussing the mechanics of the calculations – full reference details given below. The article runs through the GDP calculations, and estimates bounds on the effect of the overall growth rate due to the deflation of computers. To summarise the arguments, although it was difficult to give an exact number on the effect of differing methodologies between countries, the maximum effect was not very large.
Concluding Remarks
Unless you find yourself employed at a national statistical agency, you do not need to worry about the details of where the inflation indices are coming from. Instead, you just need to have a rough idea of the methodology and understand why they might behave differently than the prices you see in the local store.
Even in the case where you have a major interest in inflation outcomes – e.g., you are trading inflation-linked products – you just need to be able to build a forecast of the aggregate inflation index based on forecasts of components. You do not have access to the underlying measured data, and even if you disagree with the methodology for some reason, your position is marked to market based on the published numbers, not what you think they should be.
References and Further Reading
My feeling is that going to the associated national statistical agency that calculates the price index is the best source for methodology.
Economics textbooks/articles might cover some of the theoretical issues around index calculation (e.g., how to weight different items over time), but they will not necessarily reflect the details of how particular indices are calculated. Since I do not expect to ever create my own price index, I have not spent enough time pursuing that literature to offer recommendations.
The Bureau of Labor Statistics (BLS) in the United States has a “CPI home page,” and it is easy to navigate: https://www.bls.gov/cpi/. The Frequently Asked Questions page is the best introductory starting point: https://www.bls.gov/cpi/questions-and-answers.htm
Eurostat has a page for the Harmonised Index of Consumer Prices (HICP): https://ec.europa.eu/eurostat/web/hicp. As the name suggests, the HICP was created to have a single methodology for consumer price calculation in the European Union countries.
The Office of National Statistics for the United Kingdom has a page for its various price indices: https://www.ons.gov.uk/economy/inflationandpriceindices.
The Statistics Bureau of Japan has English information at this page: https://www.stat.go.jp/english/data/cpi/index.html. At the time of writing, there was a ink to a methodology guide produced in 2020: https://www.stat.go.jp/english/data/cpi/1590.html
Statistics Canada publishes “The Canadian Consumer Price Index Reference Paper”: https://www150.statcan.gc.ca/n1/en/catalogue/62-553-X. Unfortunately, there is a decent risk that the link will be broken by the time you read this, but live links should be easy to find if you search for that title.
Schreyer, Paul. “Computer price indices and international growth and productivity comparisons.” Review of Income and Wealth 48.1 (2002): 15-31. A version is available at: https://www.oecd.org/sdd/productivity-stats/30669346.pdf

Very useful as always -- distributing the link to my fellow civil servants (who one would think SHOULD but may have no understanding of this)
ReplyDelete