Effect Of A Rate Hike In A SFC Model

The effects of rate hikes on the economy is an interesting subject. There is an instinctive consensus view on what a rate hike accomplishes, but the demonstration of why this should be so is much less clear. One of the entertaining properties of SFC models is that at least some of them act in a way that is opposite to the consensus.

In this article, I simulate Model PC (Portfolio Choice) from Chapter 4 of Monetary Economics. It should be noted that this is the second simplest type of model in the book. The simulation results presented here may not apply to more advanced models. (This is why the title reads "In A SFC Models," and not the more definite "In SFC Models.") This simplicity could be viewed as the cause of the counter-intuitive results.

(Why not simulate the more complex models in the book? I am building my simulation framework, and developing algorithms to generate equations is not trivial. More complex models generate more complex errors, and so I have been building up the framework's trouble-shooting and debugging capabilities. I have finished a lot of the quality-of-life improvements, and so I am in position to attack the next class of models, which are the simple open economy models of Chapter 6. I am following the trajectory of the book as the code that generates the models is available, and so I can calibrate my results against the EViews simulations.)

As shown in the chart at the top of the article, in this simulation, there is an increase in interest rates in 1960 -- from 2.5% to 3.5%.  (The data are annual.) The economy was in a steady state before 1960, and then will move to a new steady state in response to the rate

 The chart above shows the impact of the rate hike. From 1950-1960, national output (Y) was constant (at about $106.5). One year after the rate hike (1961), national income rises. (The importance of the date of the change in output is discussed later.) It increases, until it converges towards a new steady state.

This model has no tendency towards growth. Like in Model SIM, output is mainly driven by government consumption (G), which is constant at $20 throughout the entire simulation period.

The chart above gives a clue as to why output increases. Within Model PC, the household sector holds Treasury bills (of a one-year maturity, matching the time step). The rise of interest rates in 1960 leads to higher income, and hence higher consumption. There is a multiplier effect on these increase purchases, and so national output rises.

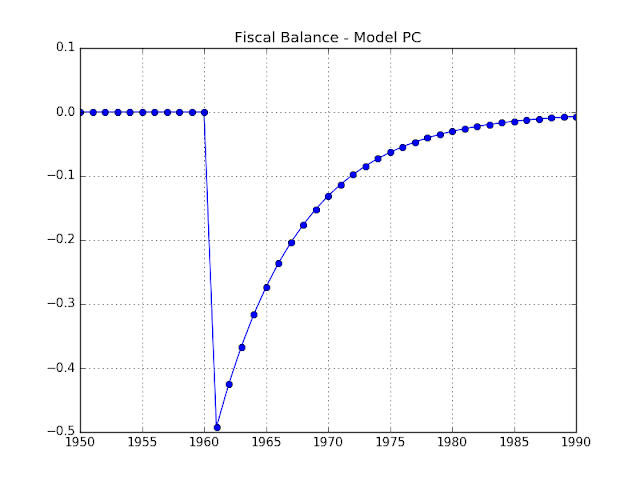
Finally, the chart above presents the government's fiscal balance. (This is equal to the primary balance less interest costs.) Within this model, the fiscal balance equals:

Fiscal balance = (Taxes) - (Government Consumption) - (Interest cost) + (Central Bank dividend).

This model separates the central bank from the Treasury. The Treasury supplies the Treasury bills (duh!), and the central bank supplies money currency. (Currency has a 0% rate of interest.)

The central bank buys Treasury bills to supply the household sector with the amount of money it desires. It generates a profit on the Treasury bill holdings, which it immediately pays to the Treasury as a dividend. The end result is that the net cost of interest for the Treasury is equal to the interest rate times the private sector's Treasury bill's holdings (which is exactly the same as if we consolidated the Treasury and the central bank).

In a SFC model without growth, the steady state government fiscal balance is $0, which we see during the 1950-1960 period. In 1961, the effect of the rate hike shows up in a greater interest bill, causing the fiscal deficit. However, increasing private sector activity raises the tax take, and so the fiscal balance converges back to $0.

The one-period delay in the reaction to the rate hike (1961 versus the hike in 1960) reflects the fact that we do not have a continuous-time model. You only get the higher interest income when the Treasury bill matures.

(As a technical note, the book and the simulation I run uses a deposit interest convention, and not a discount bill pricing convention. In a model where the interest rate is fixed by the central bank, there is no economic difference between these formalisms. The deposit convention is a lot easier to work with.)

Discussion of Results

Model PC is similar to Model SIM -- it is driven by fiscal policy. However, what matters is the entire fiscal balance, and not just the primary balance. In fact, the primary balance increased during the shock.

If we followed the fairly standard view that the stance of fiscal policy is determined by the primary fiscal balance, we would end up believing that fiscal policy tightened.  This is on top of presumably tighter monetary policy, as represented by higher interest rates and a smaller money supply (not shown; will discuss in an article on portfolio allocation).

(The way out of this apparent puzzle is to realise that the stance of fiscal policy is set by the level of government consumption and tax rates; the level of the primary balance offers us very little information.)

In other words: increasing the rate of interest increases total government spending, and there is a multiplier effect that passes through to national output.

Although interesting, it raises some awkward questions. Should central banks be raising rates rapidly in a bid to increase national income?

I am going to duck that debate, but I want to point out how these simulation results offer an incomplete picture.

• There is no modelling of the price level within the model. Interest rate policy is normally assumed to be tightly linked to inflation trends.
• This model does not incorporate longer-term government debt. Long-term bonds suffer capital losses as a result of rising yields; higher interest income will only show up as bonds mature.
• There may be further capital losses on other financial assets and real estate.
• The household sector's consumption function is independent of interest rates. (Only portfolio allocation is affected.)
• Wealth is unequally distributed; the households with large financial asset holdings may have a below-average propensity to consume out of interest income.
• There is no fixed investment (or even inventory investment) within the model. Fixed investment is presumably sensitive to interest rates.

To what extent these simulation results are misleading, I would mainly focus on the last point (fixed investment). The relative importance of these factors versus the effect of higher nominal household income on spending is an empirical matter that I do not expect to resolve here.

Technical Comments On the Python SFC Models Framework

Development is continuing, and I am now in a position to ask others for their feedback. The framework is increasingly easier to work with. At present, being able to simulate the simplest models from Monetary Economics is not going to impress people. However, it should be straightforward to progress through the other models, making the framework better positioned to be used as a teaching tool or for research purposes.

• One of the new features is hidden in the above figures. I have adapted the solver to estimate an initial steady state ("equilibrium") numerically. This eliminates the extremely messy process of setting initial conditions in SFC models (which becomes increasingly complex as we add variables).
• The only economic functionality added was the portfolio allocation framework. I will describe this later.
• Debugging support was greatly expanded, partly to deal with the problems I describe below.

I also have the ability to validate model outputs against expected results. I use this to as part of unit tests, which allow me to check that changes to code do not break functionality.

This validation surprisingly slowed me down when testing Model PC. I used spreadsheet simulations (from sfc-models.net) to provide baseline results. However, I was unable to replicate them. It took some time, but the spreadsheets appear to be slightly incorrect. (This is a rather common theme for spreadsheet-based analysis.) The clue that tipped me off to the problems with the spreadsheet is that national income changed in the same period as the interest rate rise, and not the period later. The only other variables that should change in the first period of the rate hike are the balance sheet entries that change as a result of the household portfolio shift; however, portfolio shifts do not generate income. (Unless we insert a financial sector that skims income off of portfolio shifts...)

I switched to the EViews models available on sfc-models.net to get a more robust baseline model output to match.

(c) Brian Romanchuk 2017